This is the fourth and last in a series of articles written to, a) introduce you to the most important diagrams used in object-oriented development (use case diagrams, sequence diagrams, class diagrams, and state-transition diagrams); b) describe the UML notation used for these diagrams; and c) give you as a tester a set of practical questions you can ask to evaluate the quality of these object-oriented diagrams.
In today's testing world there is good news and bad news. The good news is that, more and more, testers are being asked to evaluate the quality of object-oriented analysis and design work earlier in the development process. The bad news is that most testers do not have an extensive background in the object-oriented paradigm or in UML (Unified Modeling Language), the notation used to document object-oriented systems.
This is the last in a series of four articles written to
- introduce you to the most important diagrams used in object-oriented development (use case diagrams, sequence diagrams, class diagrams, and state-transition diagrams)
- describe the UML notation used for these diagrams
- give you as a tester a set of practical questions you can ask to evaluate the quality of these object-oriented diagrams
As in the preceding three articles, we will use three independent approaches to test these diagrams:
- syntax–"Does the diagram follow the rules?"
- domain expert–"Is the diagram correct?" "What else is there that is not described in this diagram?"
- traceability–Does everything in this diagram trace back correctly and completely to its predecessor?" "Is everything in the predecessor reflected completely and correctly in this diagram?"
For this set of articles we have been using a case study: a Web-based online auction system that I invented: f-lake. Yes, I invented the idea of online auctions. Previously I wrote that I was not sure why f-lake never caught on. I pronounced it yesterday without the "-" and now I think I understand.
State-Transition Diagrams
State-transition diagrams describe all of the states that an object can have, the events under which an object changes state (transitions), the conditions that must be fulfilled before the transition will occur (guards), and the activities undertaken during the life of an object (actions). State-transition diagrams are very useful for describing the behavior of individual objects over the full set of use cases that affect those objects. State-transition diagrams are not useful for describing the collaboration between objects that cause the transitions.
The UML notation for state-transition diagrams is shown below:
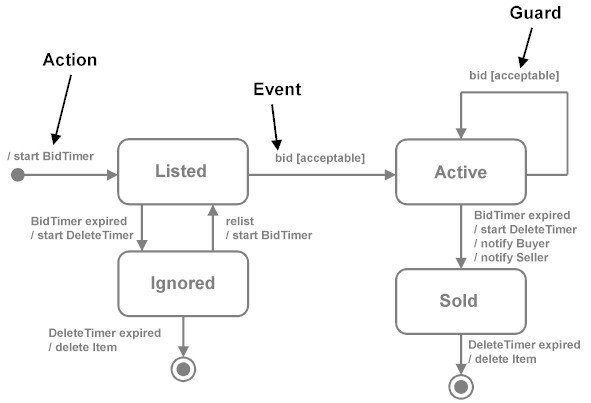
Notation
For those not familiar with the notation used for state-transition diagrams, some explanation is in order.
State. A condition during the life of an object in which it satisfies some condition, performs some action, or waits for some event.
Event. An occurrence that may trigger a state transition. Event types include an explicit signal from outside the system, an invocation from inside the system, the passage of a designated period of time, or a designated condition becoming true.
Guard. A boolean expression which, if true, enables an event to cause a transition.
Transition. The change of state within an object.
Action. One or more actions taken by an object in response to a state change.
Syntax Testing
Let's begin with the simplest kind of testing-syntax testing. When performing syntax testing, we are verifying that the state-transition diagram contains correct and proper information. We ask three kinds of questions: Is it complete? Is it correct? Is it consistent?
By now I'm sure you remember our secret from the previous articles. You do not need to know the answers to any of these questions before asking them. It is the process of asking and answering that is most important. Listen to the answers you are given. Are people confident about their answers? Can they explain them rationally? Or do they hem and haw and fidget in their chairs or look out the window or become defensive when you ask? Now for the questions:
Correct:
- Does each state-transition diagram have one and only one initial state?
- If the state-transition diagram is an open-loop, is there at least one terminal state?
- If the state-transition diagram is a closed-loop, is it really? (Almost all are actually open-loop)
- Does each state have at least one exit transition?
- If multiple guards exist for a single event, are the guards mutually exclusive?
- Does each state have exactly one transition for each possible event-guard combination?
- Have all redundant or duplicate states or transitions been removed?
- Are all states reachable?
- Is every "real" state in the world represented by one and only one state on the diagram?
- Is each state and transition clearly named?
- Are all possible paths also valid paths?
- Are all valid paths represented?
Domain Expert Testing
After checking the syntax of the state-transition diagrams, we proceed to the second type of testing-domain expert testing. Again, we have two options: find a domain expert or attempt to become one. (The second approach is always more difficult than the first, and the first can be very hard.) Continuing, we ask three kinds of questions: Is it complete? Is it correct? Is it consistent?
Complete:
- Are all of the required states, events, guards, transitions, and actions shown on the diagram?
- Are all exceptional cases handled properly?
Correct:
- Are we using state-transition diagrams only for classes that have complex, interesting behavior?
- Does the diagram correctly represent the open-loop/closed-loop nature of the class?
- Are all of the required states, events, guards, transitions, and actions properly defined?
Consistent:
- Does a one-to-one correspondence exist between an object's events and its methods?
Traceability Testing
Finally, after having our domain expert scour the state-transition diagrams, we proceed to the third type of testing-traceability testing. We want to make certain that we can trace from the requirements to the state-transition diagrams and from the state-transition diagrams back to the requirements. Again, we turn to one question: Is it consistent?
Consistent:
- Do all states, events, guards, transitions, and actions in the requirements appear in the state-transition diagram?
Conclusion
This set of questions, based on syntax, domain expert, and traceability testing; and focused on completeness, correctness, and consistency; is designed to get you started testing in an area with which you may not be familiar.
This article concludes this series on object-oriented testing. In them we've introduced you to the four most important diagrams used in object-oriented development, described the UML notation used in these diagrams, and given you a set of practical questions you can ask to evaluate the quality of these object-oriented diagrams.
I hope they have been beneficial to you.
Other articles in this series:
Use Cases: Testing UML Models, Part 1
Sequence Diagrams: Testing UML Models, Part 2
Class Diagrams: Testing UML Models, Part 3

